Brushless DC (BLDC) motors implement Hall sensors for commutation. These hall sensors produce voltage output according to rotor position [1]. Their combined outputs are used by motor drivers to sense rotor angular position and send current to the correct motor winding to obtain continuous rotation.
In one of our projects we had a BLDC motor with integrated encoder for position feedback. I happened to choose a mating connector for the encoder that has no mechanical polarization. So the connector could be attached both ways. On one careless day, which was just several days before the final project meeting and prototype demonstration, I reverse connected the connector and the encoder burned due to reverse supply voltage polarization. We contacted the motor supplier but the lead time for a new one was 6 weeks. We ordered one anyway but we had to either try to postpone the meeting or come up with a solution. Then it came to my mind that we could use the hall sensors for position feedback. The output would be very very coarse compared to the encoder, 60° resolution versus 0.35°, but luckily in this specific project we had a high gear ratio between the motor and the system to be position controlled. When divided by the gear ratio, which was around 440, you get a resolution of 60°/440=0.14° degree on output shaft which is not bad at all. At least it might save the day.
So how do you convert Hall sensor readings to motor angular position? Reading the output of three Hall sensors using an analog input card while rotating the motor shaft by hand produces the result given in Figure 1. The figure is for clockwise shaft rotation. Note that revolution per second (RPS) of motor shaft must be less than sampling frequency (fs) divided by 6 (because at every 60 degrees a Hall sensor changes state, meaning in one full turn there are 6 state changes). Otherwise the motor turns so fast that between your two consecutive sampling points you miss a Hall sensor voltage change and corrupt your sequence.
Figure 1. Hall sensor readings for clockwise rotation
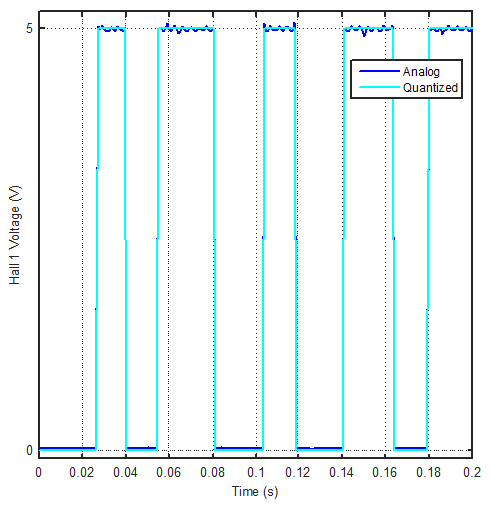
As the shaft is being rotated, the sensor outputs switch between high and low states, following a specific sequence. In order to determine the sequence, we need to follow the rising and falling edges of the signals. But before that, it would be better to convert analog signal to a discrete boolean signal and get rid of noise. Let us assume the analog voltage readings are named h1, h2 and h3 respectively. Then by defining an error margin, we get rid of the noise (Figure 2).
h_anlg = [h1;h2;h3]; % raw analog voltage signal
h_quan = h_anlg; % quantized signal
marg = 1; % a noise margin of +/- 1 volts
h_quan(abs(h_quan-5)<marg) = 5; % set all values in +/- marg vicinity of 5 volts to 5 volts
h_quan(abs(h_quan-0)<marg) = 0; % set all values in +/- marg vicinity of 0 volts to 0 volts
Figure 2. Analog Hall output is quantized to remove noise
The next step is to scale the signals between 0 and 1 by taking its sign.
h_bool = h_quan;
h_bool = sign(h_bool); % scale signal between 0 and 1.
Now we can locate rising and falling edges and determine states of each sensor for a full rotation. Let us find first the indices where signals change state.
h_bool_d = diff(h_bool,1,2);
[I,J] = find(abs(h_bool_d)>0,5);
In the code snippet above, I is the index for hall sensor and J is the index for time at which change starts. Note that the change starts at index J and new state is reached at index J+1. Now let us initialize our state vector and fill it. We know that there are 6 different states in one turn and after one turn the sequence repeats itself. Also the first state is the state at time t=0. So
states = zeros(3,6);
states(:,1) = h_bool(:,1); % first state is the state at t=0
states(:,2:6) = h_bool(:,J+1); % others are the signal levels just after an edge
For my case the states variable is obtained as follows.
states =
0 0 0 1 1 1
0 1 1 1 0 0
1 1 0 0 0 1
You can reach the same conclusion by looking at Figure 1 directly. In Figure 1, the starting state is 0, 0, 1. Out of the three signals, first the red one changes state and the next state is 0, 1, 1 etc. But the code automates the process.
Now that we obtained the sequence we can create a Simulink model and convert these signals to motor angle. We first need to determine which state we are in at start-up, then at each sample time, check our new state. If the new state is to the right of the previous state in our sequence table, the motor turned clockwise 60 degrees (note that we collected the data and generated the sequence for a clockwise rotation). If the new state is to the left of the previous state in our sequence table, the motor turned counter-clockwise 60 degrees. If the new state jumped more than one state compared to previous state, then the motor turned too fast with respect to our sampling frequency and we missed an unknown amount of state changes. In this case we get an error that builds-up in our motor angle conversion. We either accept this error or throw a warning/exception. In Figure 3, a sample Simulink model is shown. You can use a Stateflow block to implement the algorithm defined in this paragraph or you can write a Matlab function as I did.
Figure 3. Sample Simulink model that converts simulated hall sensor outputs to motor angular position
The MATLAB Function block has two inputs v and u. v is the 3x6 states matrix obtained above. u is a 1x5 vector whose first three elements are boolean hall sensor signals h (take care of the ordering), the fourth element is a scalar s that shows current state, and the last element is a counter c for determining motor angle. The output of the block are scalars s and c which are fed back to the block as input to be used for the next sampling time. The blocks inside yellow region simulate the BLDC motor sensor outputs. Slider Gain block can be adjusted between +/- 720 degrees and is used to simulate motor shaft rotation. In the actual application the blocks inside the yellow region should be replaced by the analog input card. The Quantizer and Sign blocks just before the MATLAB Function block convert noisy analog signals to boolean signals. The counter output c of MATLAB Function block is multiplied by 60 to convert the counter to motor angular position in degrees. The code inside MATLAB Function block is as follows.
function y = fcn(v, u)
h=u(1:3); % boolean hall sensor signals
s=u(4); % switch indicating current state
c=u(5); % counter
sta = v'; % copy states matrix
if (s==0) % initially s==0
c = 0;
if (all(h==sta(1,:)))
s = 1;
elseif (all(h==sta(2,:)))
s = 2;
elseif (all(h==sta(3,:)))
s = 3;
elseif (all(h==sta(4,:)))
s = 4;
elseif (all(h==sta(5,:)))
s = 5;
elseif (all(h==sta(6,:)))
s = 6;
end
else
nxt = mod(s,6)+1; % next state column index
pre = mod(s-2,6)+1; % previous state column index
if (all(h==sta(nxt,:))) % current state is to the right of prev state
s = nxt;
c = c+1;
elseif (all(h==sta(pre,:))) % current state is to the left of prev state
s = pre;
c = c-1;
else
% you missed a state change. raise warning/error or do nothing.
end
end
y=[s,c];
Using the code above, we were able to sufficiently control our prototype (of course we had to implement some other algorithms such as dead zones to prevent chattering and limit cycles etc.). We were able to postpone the final meeting and demonstration to a much later time but it did us no good because to this day we still couldn't receive the replacement motors yet. We demonstrated the project explaining the situation and our project was approved. The moral of the story is that think ahead and always buy spares because accidents and mistakes happen.
REFERENCES:
[1] http://www.parkermotion.com/manuals/OEM770T/5_Hall_Effects_770T.pdf